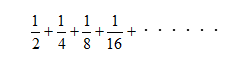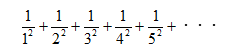「どんなに小さなことでも、積み重ねていくと大きな結果となる」

いわずと知れた有名なことわざです。

 

さて、数学の世界では「塵が積もっても大した結果にならない」なんてことが多々あります。

特定の規則に従って決められた数の並び（＝数列）を順に加えたときに、その和が一定の数に限りなく近づいていくことがあり、これを「和が収束する」といいます。

例えば、次のような式は・・・

 

この式は、計算結果がなんと１に収束してしまいます。

（ぜひ理由を考えてみてください、図を描くとイメージしやすいかも？）

 

 

かつて、このような無限に続く数列の和に関する研究を成し遂げた偉大な数学者がいました。

彼の名は、レオンハルト・オイラー（1707年～1783年）といいます。

オイラーは、問題の提起から91年もの間いかなる数学者も解くことのできなかったある問題の解を得ることに成功します。

↓↓↓↓↓↓↓↓↓↓↓↓

 

いたってシンプルな、平方数の逆数の和ですが、じつはこの問題は多くの数学者を苦しめた、「バーゼル問題」という問題です。

 

この問題の答えを理解するには、高校の数学知識をフル活用する必要があります。

大学入試でも出題されたことのある有名な問題です。

ぜひ、チャレンジしてみてください。

 

たまにはこうして、先人たちの叡智に触れるのも良いものですね。

 

ステップ個別指導学院　北高崎駅前校　山浦

TEL: 027-386-4134（午後２時～７時）

E-mail: step.kitatakasaki@gmail.com（24時間365日OK）